Leetcode 671 Second Minimum Node In a Binary Tree

671. Second Minimum Node In a Binary Tree

Second Minimum Node In a Binary Tree

Problem Statement

Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.

Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

If no such second minimum value exists, output -1 instead.

Examples

Example 1:

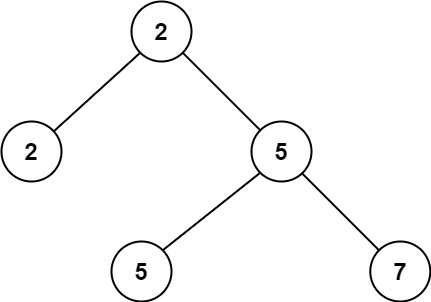
Input: root = [2,2,5,null,null,5,7]
Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.

Example 2:

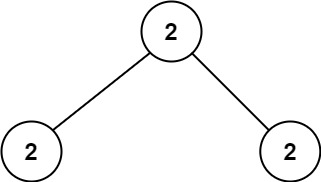
Input: root = [2,2,2]
Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.

Constraints

The number of nodes in the tree is in the range [1, 25].
1 <= Node.val <= 2³¹ - 1
root.val == min(root.left.val, root.right.val) for each internal node of the tree.

Solution

We will define a recursive helper function to solve this problem.

The function accepts a node and a min value as parameters. It returns the smallest value that’s greater than the given min value.

At each of the recursion, we check the following the things:

Am I null? If yes, return -1. This is the end condition for the recursion.
Am I greater than the min value passed in?
- If yes, return my value.
- If no, it definitely means my value is equal to the min value passed. Check my left and right child with the same helper function with my value as the min value. Compare the result and return corresponding value.
  - If any of the child returns -1, it means it does not have a value that’s greater than the min value passed in, we can just simply return the other child’s result.
  - If both child’s results are -1, we return -1
  - If both have a positive result, we return the smaller one.

Python:

def findSecondMinimumValue(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        def helper(node, min_val):
            if not node:
                return -1
            
            if node.val > min_val:
                return node.val
            else:
                left = helper(node.left, min_val)
                right = helper(node.right, min_val)
                if left == -1 and right > 0:
                    return right
                elif right == -1 and left > 0:
                    return left
                elif left > 0 and right > 0:
                    return min(left, right)
                else:
                    return -1
        
        return helper(root, root.val)

Java:

class Solution {
    public int findSecondMinimumValue(TreeNode root) {
        
        int helper(TreeNode node, int minVal) {
            if (node == null) {
                return -1;
            }
            
            if (node.val > minVal) {
                return node.val;
            } else {
                int left = helper(node.left, minVal);
                int right = helper(node.right, minVal);
                if (left == -1 && right > 0) {
                    return right;
                } else if (right == -1 && left > 0) {
                    return left;
                } else if (left > 0 && right > 0) {
                    return Math.min(left, right);
                } else {
                    return -1;
                }
            }
        }
        
        return helper(root, root.val);
    }
}

Time Complexity:
The time complexity is O(n)since we will be visiting all the nodes in the tree in the worst case.

Space Complexity:
The space complexity is O(h) where h is the height of the tree. This is because we are using DFS to traverse the tree. The max stack size depends on the height of the tree.

Leetcode 671 Second Minimum Node In a Binary Tree